☆ 演習6−3 ☆(選択ソート)
6つの数値を入力すると、自動的に昇順(小さいものから大きいものへ)に整列するアルゴリズムを作成しなさい。
ただし、整列アルゴリズムには「選択ソート」を用いること。
ここからはいろいろなソートについて学んでいきます。
始めはまず選択ソート。
では、選択ソートとはいったいどういったものなのでしょうか・・・
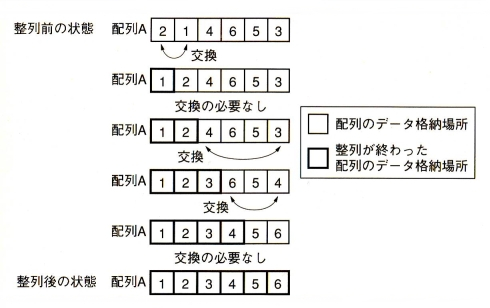
この図が選択ソートのイメージになります。
選択ソートは、「基本選択法」とも言います。
今回の演習のように昇順に整列するアルゴリズムの場合、選択ソートは常に最小値を検索し、発見した時点でそのデータと整列の終わっていないデータを入れ替えるという処理を繰返すものです。
整列の終わったデータは参照されず、固定されます。
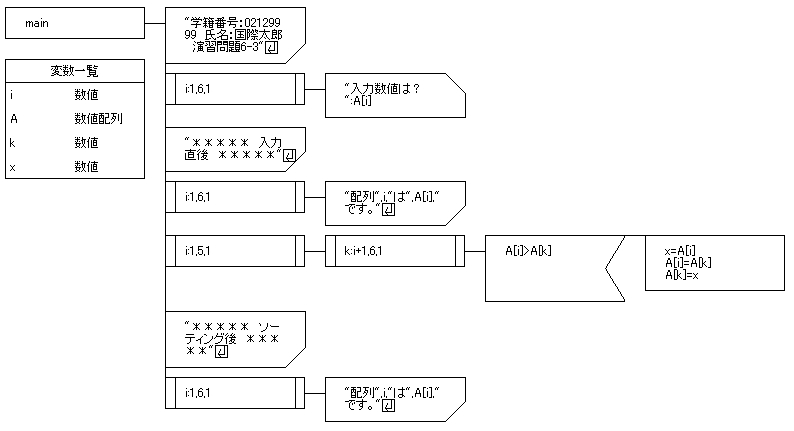
そして作成するシートはこちら。
少しずつ分割して説明していきましょう。
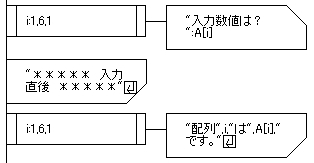
ここは前回までの課題を終えている人でしたら問題ないはずです。
6回入力させて、それを全て配列に入れています。
そしてそれを入力された順番通り出力しているだけです。
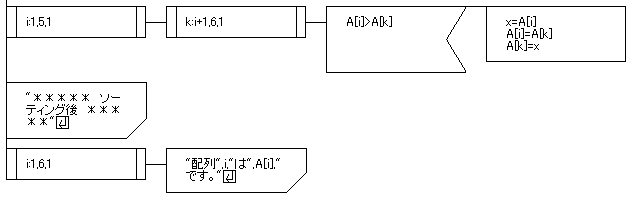
この部分。
この部分の条件値判定シンボルの横に配置されている3つのシンボルが選択ソートの部分になります。
『k:i+1,6,1』と言う条件値ですが、これはkがi+1から6になるまで1を足していくという意味ですよね。
この時点で、kが2から始まっているということがわかりますか?
なぜかというと、iはまず1から始まっています。
それに+1をしているのがkになっているからです。
そこまで理解できましたら次の分岐処理。
『A[i]>A[k]』ですが、これは上の一文を理解できたのならわかるはずです。
A[i]というのは、iが1ですから配列の一番目を、A[k]というのは、kが2ですから配列の二番目を参照していますね。
ですので、まずは最初に入力された数値と二番目に入力された数値を比較しているのです。
そして、今回は昇順ですから、一番目の数値が二番目の数値より大きければ入れ替えが必要です。
そこで、まずA[i]をxという変数に入れておいて、A[i]のところにはA[k]を入れます。
最後に、xに入れておいたA[i]をA[k]に入れるのです。
ちょっと解りにくいですね。
今解説している一番目と二番目の比較だけ、数値にして説明してみます。
まず、一番目に入力した数値(A[1])を変数xに置いておきます。
次に一番目に入力した数値のところに二番目に入れた数値(A[2])を入れます。
変数xが必要な理由は、一番目に入力した数値のところに二番目の数値を入れてしまったら、一番目の数値は消えてしまいますよね。
それではソートができなくなってしまいますので、退避場所として変数がひとつ必要になるからです。
そして最後に二番目に入力した数値のところに変数xに入れた一番目に入力した数値を入れれば、入れ替えは完了です。
あとは、iに1を足しながら配列を移動して、これを繰返しているだけです。
そして最後にソートが完了した順番で出力したらokです。
では、実行してみましょう。
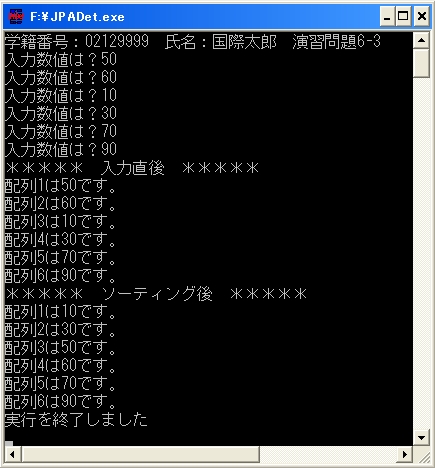
まず6つの数値を入力します。
すると、まずは入力された順番出力されていますね。
しかしその下は入力された数値がしっかりと昇順となり出力されました。
ちなみに、降順(数値が大きい方から小さい方へ)の場合は、ソート内の分岐シンボルの中の『A[i]>A[k]』という式を、『A[i]<A[k]』とすればいいだけですね。
(もしくは、条件が「真」だった場合に処理させるのではなく、「偽」の場合に処理させてもok)