☆ 演習7−2 ☆(バイナリ探索)
特定の数値を入力すると、その数値があらかじめ用意されたデータ郡のどこにあるのかを調べるアルゴリズムを作成しなさい。
ただし、その探索のアルゴリズムには「バイナリ探索(二分探索)」を用いること。
探索アルゴリズムの二つ目です。
今回は『バイナリ探索』を解説していきます。
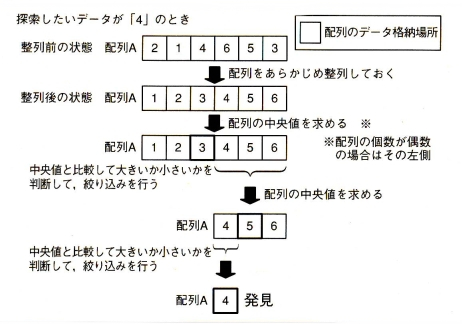
この図がバイナリ探索のイメージになります。
バイナリ探索は、「二分探索」とも言います。
バイナリ探索は、配列をあらかじめ整列しておくことから始めます。
探索が開始されると、配列の中央にあたるデータの格納場所を求めて、そのデータよりも探索したいデータは大きいのか小さいのかを判断して、範囲を絞り込んでいきます。
そして、この処理を連続して行うことでデータを発見するのです。
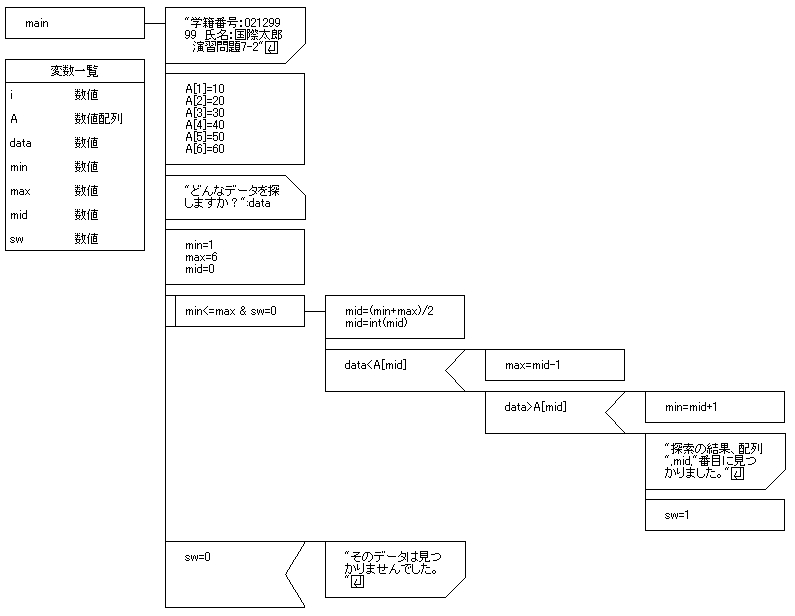
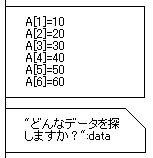
まず、配列に任意の数字を入れておきます。
ここまでは演習7-1と同じです。
そして、探したいデータを入力させたら、それを変数dataに入れておきます。
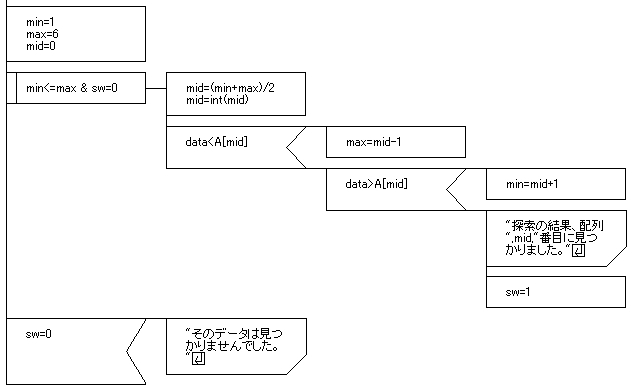
少し大きくなってしまいましたが、ここの前判定繰返しシンボルとその右に配置されているシンボルがバイナリ探索の部分になります。
バイナリ探索は、配列が整列した状態から始めることはもう説明しましたね。
ですので、数値はしっかりと順番に並んでいるということです。
配列の数は6つ。
配列の一番初めは1、最後は6ですよね。
ですので、minに一番小さい数値の1を、maxに一番大きい数値の6が入っています。
真ん中のmidはまだわからないので0を入れておきます。
ではここからバイナリ探索スタートです。
まず、『min<=max & sw=0』ですが、minの数値がmax以下で、swが0の場合は繰返すという意味ですよね。
(ちなみに、後で説明しますがswはデータが見つからない限り0のままです)
次に、minとmaxを足して2で割り、midを設定します。
そして、入力されたデータが配列の真ん中(mid)のものより小さければ、それよりも大きい数値の配列部分は必要ないですので、midをmaxに設定します。
入力されたデータが、配列の真ん中(mid)より大きければ、midより小さい配列部分は必要ありませんよね。
この作業を繰返すのです。
入力されたがmidより大きいか小さいかで、mid以下もしくはmid以上の配列部分を除外していきながら少しずつ範囲を狭めて、目的の数値を見つけます。
少々解りづらい探索なので、このページの一番上に配置されているバイナリ探索のイメージ図をみながら少しずつ理解していきましょう。
目的の値が見つかると、それを出力してswに1を入れます。
swが0以外になるとこの判定繰り返しからは抜け出しますよね。
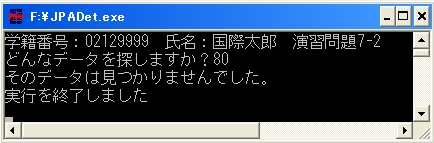
そして、もし見つからなかったらswが0のまま抜け出します。
その場合は、最後に『そのデータは見つかりませんでした』と出力させるのです。
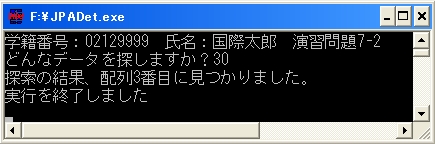
では、実行結果はどうなったでしょうか。
配列に入っている数値を入力した場合と、配列に入っていない数値を入力した場合です。
探索方法は違いますが演習7-1と同じ出力結果です。
理解してしまえばどうということはないですが、バイナリ探索は線形探索よりわかりにくいですので、あわてず一つ一つのシンボルずつゆっくりと理解していきましょう。